Classifier-Guided Diffusion论文阅读

发表于 2023-01-04 更新于 2023-01-07 分类于论文阅读阅读次数：本文字数： 4.5k 阅读时长 ≈ 16 分钟

Classifier-Guided Diffusion介绍

论文：Diffusion Models Beat GANs on Image Synthesis Prafulla Dhariwal Alex Nichol

这篇论文主要做了两方面的工作：第一个方面是对模型（U-Net）的架构做了一些改进；第二个方面是提出了一种给扩散模型加入条件信息的方法。其中，第二个方面是我们关注的重点。

预备知识：多维高斯分布

在介绍论文之前，先对多维高斯分布有一个清晰的认识。

我们熟悉一维高斯分布的形式：而高维的高斯分布（互相独立）我们用矩阵的形式表示：为什么独立多维高斯分布可以表示为这种形式呢？我们来推导一下：

先假设个变量互不相关，且服从正态分布（维度不相关多元正态分布），各个维度的均值，方差。

由于各个变量相互独立，联合概率分布可以写作：令 $，$ 这样多元正态分布又可以写成一元那种漂亮的形式了：因为多元正态分布有着很强的几何思想，单纯从代数的角度看待很难看出的概率分布规律，这里需要转换成矩阵形式：我们做一下变量替换：

代表变量的协方差矩阵，行列的元素值表示与的协方差。因为现在变量之间是相互独立的，所以只有对角线上 ()存在元素，其他地方都等于0，且与它本身的协方差就等于方差。

是一个对角阵，根据对角矩阵的性质，它的逆矩阵：对角矩阵的行列式 = 对角元素的乘积，所以替换变量之后，等式可以简化为：代入以为自变量的标准高斯分布函数中：

这样就得到了多维高斯分布的概率密度的表达式。

下面是二维高斯分布的概率密度的可视化图像：

条件控制生成

条件控制生成一直以来是生成模型关注的一个重点。作为生成模型，扩散模型跟VAE、GAN、flow等模型的发展史很相似，都是先出来了无条件生成，然后有条件生成就紧接而来。无条件生成往往是为了探索效果上限，而有条件生成则更多是应用层面的内容，因为它可以实现根据我们的意愿来控制输出结果。从DDPM至今，已经出来了很多条件扩散模型的工作，甚至可以说真正带火了扩散模型的就是条件扩散模型，比如脍炙人口的文生图模型DALL·E 2、Imagen。

从方法上来看，条件控制生成的方式分两种：事后修改（Classifier-Guidance）和事前训练（Classifier-Free）。

对于大多数人来说，一个SOTA级别的扩散模型训练成本太大了，而分类器（Classifier）的训练还能接受，所以就想着直接复用别人训练好的无条件扩散模型，用一个分类器来调整生成过程以实现控制生成，这就是事后修改的Classifier-Guidance方案；而对于像Google、OpenAI等大型公司来说，它们不缺数据和算力，所以更倾向于往扩散模型的训练过程中就加入条件信号，达到更好的生成效果，这就是事前训练的Classifier-Free方案。

Classifier-Guidance方案最早出自《Diffusion Models Beat GANs on Image Synthesis》，也就是本篇文章，最初就是用来实现按类生成的；后来《More Control for Free! Image Synthesis with Semantic Diffusion Guidance》推广了“Classifier”的概念，使得它也可以按图、按文来生成。Classifier-Guidance方案的训练成本比较低（熟悉NLP的读者可能还会想起与之很相似的PPLM模型），但是推断成本会高些，而且控制细节上通常没那么到位。

至于Classifier-Free方案，最早出自《Classifier-Free Diffusion Guidance》，后来的DALL·E 2、Imagen等吸引人眼球的模型基本上都是以它为基础做的，值得一提的是，该论文上个月才放到Arxiv上，但事实上去年已经中了NeurIPS 2021。应该说，Classifier-Free方案本身没什么理论上的技巧，它是条件扩散模型最朴素的方案，出现得晚只是因为重新训练扩散模型的成本较大吧，在数据和算力都比较充裕的前提下，Classifier-Free方案变现出了令人惊叹的细节控制能力。

接下来我们看一下这篇论文中是如何加入条件信息的。

条件扩散过程

我们首先定义一个类似于的条件马尔可夫噪声过程，并假设是每个样本的一个已知的和容易获得的标签分布。下面是我们的一些定义：经过了上面的定义之后，我们可以进行一系列的推导证明，证明没有基于的条件下，和的表现完全相同。

首先推导：

注：第一行引入隐变量，第二行是将联合分布拆成（条件分布×边缘分布）的形式，第三行利用定义，第四行提出与积分变量无关的因子，第五行利用概率密度的性质。

可以看到，就像上面说到的，没有基于的条件下，和的表现完全相同，即。

接下来推导：

注：第一行也是引入隐变量，第二行也是将联合分布拆成（条件分布×边缘分布）的形式，第三行利用了定义中的马尔可夫性，第四行也是用定义替换，第五行提出积分无关因子，第六行同样利用概率密度的性质，第七行则是利用原始的前向过程的马尔可夫性。可以看到，推导思路与上面的几乎完全一样。

可以看到，进一步验证了上面的说法，。

接下来继续推导：

注：第一行也是引入其他变量进行积分，第二行也是将联合分布拆成（条件分布×边缘分布）的形式，第三行则是利用定义和上面证出的结论进行替换，第四行是将原始前向过程的（条件分布×边缘分布）形式变回联合分布的形式，最后做积分得到。思路和前面几乎还是没有半分区别。

同理，遵循同样的思路加上贝叶斯定理，我们也可以轻松的推出。

还有一个有趣的现象，就是这个含噪声的分类函数并不依赖于（比噪声程度更大），证明如下：

注：第一行是贝叶斯定理，第二行是我们刚才证明的结果。

有了上面的一系列推导，现在我们可以得到带条件的反向过程的表达式了，如下所示：

注：第一行是将条件概率写成（联合概率÷边缘概率）的形式，第二行将分母中的联合概率改写为（条件×边缘），第三行则是将分母展开，第四行进行约分，第五行利用刚才证明的性质，第六行则是对刚才证明的结果进行替换。

现在我们就得到了带条件的反向过程的表达式：

可以看到，分母可以看做常数，因为它不依赖于，可以记作。因此我们想从分布中采样，其中是归一化常数。我们已经训练了一个用来近似的神经网络，所以只剩下一个，它可以由我们训练好的带噪声的分类器得到。

条件反向过程

经过了上面的推导，我们可以得到条件反向过程可以建模为从如下分布中采样：直接对上述分布进行采样可能还是有困难，因此我们可以做一个近似处理。

我们之前已经建模了（这里用到预备知识中的多维高斯分布）：接下来，我们求，我们可以对在处进行泰勒展开，来得到它的近似：其中，，是常数。

这样，我们就可以得到如下的表达式：注意，从第一行推第二行是一个难点。我们可以对第二行进行展开，验证可以得到第一行的公式。在这里，经过我和我的一个朋友的推导验证，发现原论文里似乎漏掉了一个转置符号，在这里用红色字体进行了标注。

这样，从原分布中采样就可以近似的等价于从中进行采样。

DDIM的条件采样

上述条件采样的推导仅适用于随机扩散抽样过程，不能应用于DDIM等确定性抽样方法。为此，我们使用了来自基于分数的条件扩散技巧，它利用了扩散模型和分数匹配之间的联系。两者之间的核心联系是：这样，我们可以进行这样的替换：这样我们就可以定义一个新的：然后，我们可以使用与常规DDIM完全相同的采样程序，但使用修改后的噪声预测，而不是。

缩放分类器梯度

为了增加条件生成图片的准确程度，我们给分类器梯度前面加上一个大于1的系数，即。这样做的原理是，，当时，的分布比更尖锐，因为较大的值被指数放大。换句话说，使用更大的梯度尺度更关注分类器的模式，这可能是产生更高质量（但较少多样性）样本的理想条件。

采样算法

DDPM条件采样算法

DDIM条件采样算法

实验结果分析

各类指标与梯度尺度因子的关系

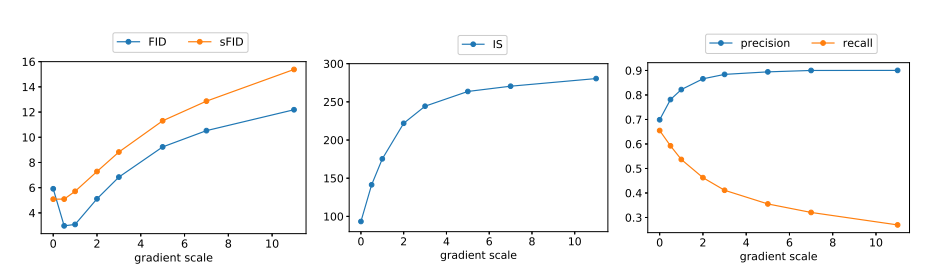
可以看到，随着梯度尺度因子的不断增加，生成的图像的质量在不断增加（体现为IS和precision不断增加），图像的多样性在减小（体现为FID后期和recall不断减小），印证了上文中对于的分析。

与BigGAN的对比

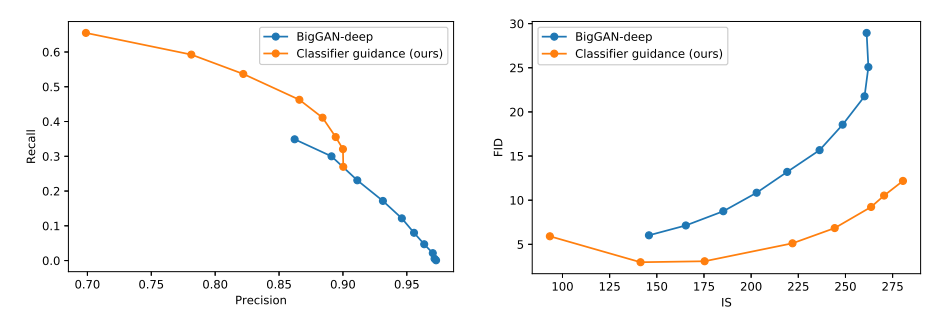
可以看到，对于第一幅图，为了保证图像的质量和多样性都尽可能高，曲线越靠近右上方意味着模型越好。对于第二张图，则是越靠近右下方，模型越好。在第一幅图里，本论文中的扩散模型的曲线在BigGAN的右上方，在第二幅图里，扩散模型的曲线在BigGAN的右下方，说明在图像的质量和多样性这两个指标上，扩散模型超越了GAN，这与标题Diffusion Models Beat GANs on Image Synthesis相对应。